Pytanie stare jak świat. Co więcej, istnieje nawet na temat dzielenia przez zero popularna rymowanka: ,,pamiętaj cholero nie dziel przez zero!”. Ok, ale właściwie dlaczego? Większość z was słyszała pewnie w odpowiedzi: ,,bo tak”. Nie jest to jednak zadowalające wyjaśnienie. Pozwólcie zatem, że wyjaśnimy Wam dlaczego taka operacja nie jest możliwa.
Przykład:
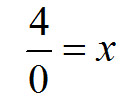
Załóżmy na chwilę, że takie dzielenie jest możliwe. Wówczas liczba 4 dzielona przez 0 powinna nam dać jakąś konkretną wartość, oznaczoną za pomocą niewiadomej „x”. Ok, poszukajmy więc tej niewiadomej. Dokonajmy na samym początku prostego przekształcenia równania tj. pomnóżmy obie strony równania przez zero. Dzięki temu pozbędziemy się mianownika z lewej strony. Sprawdźmy:
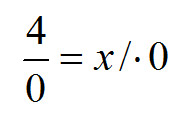
![]()
I tu pojawia się zasadniczy problem. Szukamy takiej liczby „x”, która pomnożona przez zero da nam liczbę 4. Niestety, jak wiadomo taka liczba nie istnieje, ponieważ cokolwiek pomnożymy przez zero, zawsze otrzymamy 0! Wychodzi nam zatem sprzeczność: 4 = 0.
No dobrze. Pewnie i tak ktoś by wymyślił, że przecież można zapisać taki oto przykład:
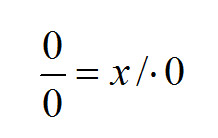
Co daje: 0 = x * 0, więc 0=0 !
Wydawać by się mogło, że wszystko jest ok, jednak pojawia się tutaj inny problem. Korzystając z własności, że z równaniem możemy robić co chcemy, pod warunkiem jednak, że daną operację przeprowadzamy obustronnie i jednocześnie - to rozważmy następującą sytuację:
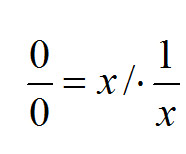
Otrzymujemy zatem:
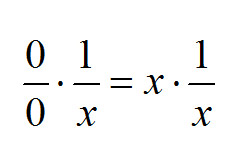
Lewa strona według wcześniejszego założenia da zero a prawa po skróceniu licznika z mianownikiem da 1. Otrzymujemy tutaj równanie 0 = 1, które jak widać nie jest prawdziwe!
Mamy nadzieję, że powyższe przykłady pozwoliły Ci zrozumieć dlaczego dzielenie przez 0 jest niewykonalne :)






Komentarze