Zaczynamy temat: funkcja kwadratowa wzory :) Temat został podzielony na kilka lekcji. W tej zajmiemy się samymi podstawami tzn. porozmawiamy o wzorach i o tym jak przechodzić z jednej postaci do drugiej. Zaczynamy!
Funkcja kwadratowa - postać ogólna
Pierwszą postacią funkcji kwadratowej jest jej postać ogólna, którą wyrażamy wzorem:
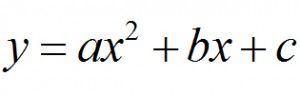
W odróżnieniu od funkcji liniowej w której były dwa współczynniki tutaj tj. w funkcji kwadratowej mogą wystąpić trzy współczynniki. Współczynnik „a” czyli tak zwany współczynnik kierunkowy określa nam w którym kierunku są skierowane ramiona paraboli. Jeśli współczynnik „a” jest dodatni to ramiona są skierowane w górę, jeśli natomiast jest ujemny to ramiona skierowane są w dół. Współczynnik „b” jest w zasadzie wykorzystywany tylko w poszczególnych wzorach tyczących się funkcji kwadratowej. Wyraz wolny „c” identycznie jak w funkcji liniowej określa nam miejsce przecięcia z osią Y.
Patrząc na funkcję już z grubsza jesteśmy w stanie mniej-więcej wykonać jej poglądowy szkic, który w toku rozwiązywania naszego zadania zawsze będzie można zmienić. Szkic ma za zadanie pokazać nam poglądowo jak dana funkcja może wyglądać. Tą metodą jesteśmy w stanie szybciej wpaść na pomysł jak rozwiązać zadanie, niż gdybyśmy starali się wykonywać wszystkie operacje jedynie w naszej głowie :) Możemy zatem już pokusić się o wstępny wykres funkcji, wykorzystując tylko te informacje, które mamy TU i TERAZ co oznacza, że w naszym zadaniu możemy już teraz odczytać dwie, następujące rzeczy: - jak skierowane są ramiona - gdzie funkcja przecina oś Y
![]()
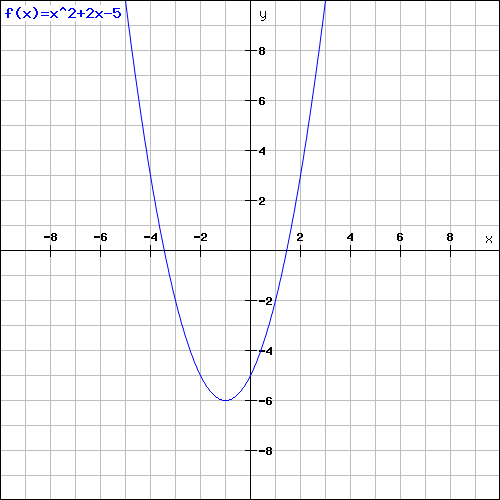
Tyle informacji wystarczyło nam, żeby zrobić wykres poglądowy funkcji (powyższy wykres jest oczywiście bardzo dokładny, gdyż został wygenerowany w programie :) ) Podczas kolejnych zajęć dowiesz się jak i kiedy przydać mogą się nasze pobieżne wykresy funkcji.
Poniżej wzory jakie powinieneś na tym etapie opanować:
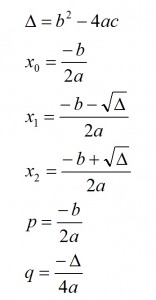
Zapomnij jednak o szkolnej definicji mówiącej, że ZAWSZE liczymy deltę. Nie jest to prawda. Delta jest nam potrzebna tylko do obliczeń w niektórych zadaniach z brakującym parametrem, we wzorze na „q” oraz do miejsc zerowych - przy czym w miejscach zerowych często nie musimy jej liczyć wcale, istnieją bowiem prostsze sposoby :) No ale o tym w kolejnej lekcji w której będziemy liczyć miejsca zerowe. Na chwilę obecną wystarczy, że zrozumiesz wzory z tej lekcji.
Poniżej krótkie objaśnienia wzorów.
Wzór na deltę wykorzystuje WSZYSTKIE trzy współczynniki z postaci ogólnej. Pamiętaj, że jeśli nie ma jakiegoś współczynnika to znaczy, że wynosi on 0. Dla przykładu: y = 2x^2 – 4. Funkcja ta nie posiada niewiadomej „x” w pierwszej potędze zatem współczynnik b = 0. I teraz w zależności od tego jaka wyjdzie delta jesteśmy w stanie określić ile miejsc zerowych posiada funkcja lub czy ich nie posiada. Pamiętajmy, że: - jeśli delta wychodzi dodatnia tzn. że funkcja posiada dwa miejsca zerowe (przecina oś X w dwóch miejscach), - jeśli delta jest równa 0 to funkcja posiada jedno miejsce zerowe (dotyka wierzchołkiem osi X),
- jeśli delta jest mniejsza od zera to brak miejsc zerowych (funkcja w żadnym punkcie nie przecina ani nie dotyka osi X).
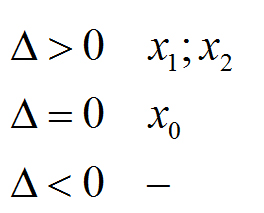
Wzory na „p” i „q” to wzory pozwalające obliczyć współrzędne wierzchołka paraboli. Nasze „p” tyczy się osi X, natomiast „q” osi Y. Warto zauważyć, że wzór na „p” oraz x0 są identyczne. Dzieje się tak dlatego, ponieważ jeśli funkcja ma jedno miejsce zerowe to styka się ona wierzchołkiem z osią „x” dokładnie w swoim środku! Skoro dokładnie środkiem dotyka naszej osi a jej środek to tak naprawdę współrzędne „p” i „q”. Stąd właśnie identyczny wzór. Jeśli jesteśmy już przy wzorze na „p” to zapamiętaj także, że jest to SYMETRALNA naszej paraboli (zawsze). Symetralna jest to prosta (pionowa), która dzieli nam naszą funkcję na dwie identyczne połowy. Jeśli więc w zadaniu będzie podane, że równanie x=5 jest SYMETRALNĄ funkcji kwadratowej tzn. że na tacy mamy podaną współrzędną „p” wierzchołka :)
Współrzędna „q” natomiast określa nam jak nisko lub jak wysoko sięga nasza parabola. W zależności od tego w którą stronę skierowane są ramiona wskazuje nam nasz maksymalny bądź minimalny Y, który wykorzystujemy przy określeniu zbioru wartości. Jeśli więc w zadaniu ktoś nam poda informację, że zbiorem wartości funkcji kwadratowej jest przedział (-00 ; 12) to już mamy dwie cenne informacje! Po pierwsze wiemy, że nasze „q” jest równe 12. Wiemy także, że ramiona muszą być skierowane w dół ponieważ funkcja ta nie posiada minimalnego „y” - wynosi on minus nieskończoność.
Postać kanoniczna funkcji kwadratowej
Postać kanoniczna funkcji kwadratowej opisana jest wzorem:
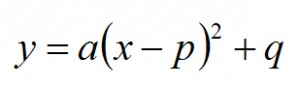
Podobnie jak w przypadku postaci ogólnej posiadamy tutaj współczynnik kierunkowy. Jesteśmy więc w stanie określić kierunek ramion. Z postaci tej możemy także odczytać współrzędne wierzchołka. Nasz poglądowy wykres funkcji będzie więc troszkę dokładniejszy niż w przypadku funkcji w postaci ogólnej :) Zatem jeśli będziesz widział taką postać to powinieneś na swój wykres nanieść od razu współrzędne wierzchołka i od niego w odpowiednim kierunku narysować ramiona paraboli. Przykład:
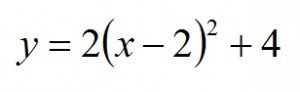
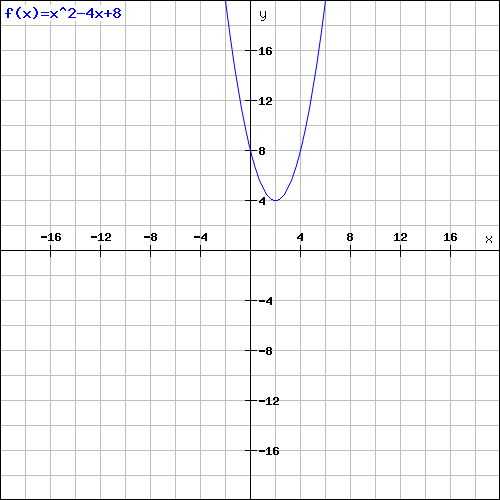
Mając postać kanoniczną dostajemy od razu dużo informacji. W treści zadania podają nam bowiem zbiór wartości funkcji (gdyż znamy wierzchołek) oraz równanie symetralnej odcinka. Co więcej - znając „p” (ew. symetralną lub x0) jesteśmy w stanie podać monotoniczność funkcji (ale o tym opowiemy wam dokładniej w kolejnej lekcji).
Postać iloczynowa funkcji kwadratowej
Postać iloczynowa funkcji kwadratowej wyrażona jest wzorem:
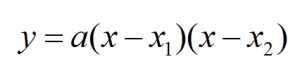
Tak jak poprzednio, tak i w tej postaci posiadamy współczynnik kierunkowy. Dodatkowo znamy również miejsca zerowe funkcji! Te dwie informacje powinieneś więc zawsze od razu nanieść na swój wykres poglądowy. W tym miejscu od razu wyjaśnię, że znając funkcję kwadratową w postaci iloczynowej znamy punkty przecięcia z osią „x”, dzięki czemu będzie można określić gdzie funkcja jest większa od 0 lub mniejsza :)
Przykład wykresu poglądowego dla funkcji y = 3(x - 1)(x + 1)
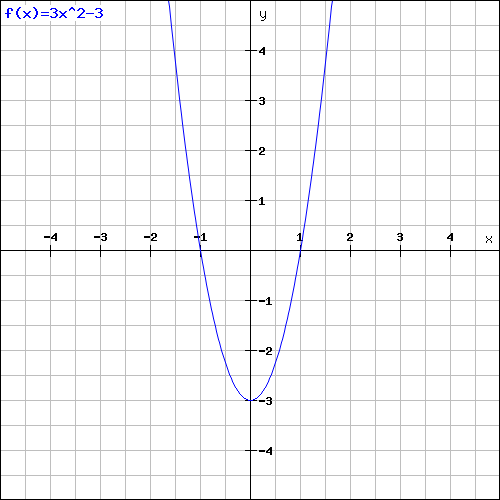
Tym oto sposobem kończymy pierwszą lekcję o funkcjach kwadratowych a dokładniej "funkcja kwadratowa wzory", która była tak naprawdę tylko wstępem :) Przyswój sobie wiadomości, które dziś przekazaliśmy, wymyśl kilka funkcji w różnych postaciach i spróbuj sporządzić ich wykresy.
Do zobaczenia na kolejnej lekcji!





Komentarze