Temat na dziś to funkcja liniowa przechodząca przez punkt. W ostatniej już części poświęconej funkcji liniowej zajmiemy się bowiem funkcjami przechodzącymi przez podane punkty oraz sprawdzaniem czy dany punkt należy do naszej funkcji. Tak więc zaczynamy! :)
Funkcja liniowa przechodząca przez punkt - Czy punkt należy do wykresu funkcji?
Pytanie, które pojawia się dość często a jeszcze nie zostało przez nas poruszone. Zanim sobie jednak na nie odpowiemy musimy Ci coś wyjaśnić. W matematyce istnieje określone stwierdzenie, że dana rzecz jest prawdziwa lub fałszywa czyli mówimy o niej: PRAWDA lub FAŁSZ. (ciekawostka: można to oznaczyć sobie także binarnie jako: PRAWDA -> 1 ; FAŁSZ -> 0.) Czyli albo coś jest albo czegoś nie ma. Na tej podstawie dokonuje się obliczeń, pozwalających sprawdzić jakąś zależność, gdzie w wyniku końcowym otrzymamy właśnie potwierdzenie naszej tezy lub jej zaprzeczenie.
No dobrze, ale jak to się ma do funkcji liniowej? Rozpatrzmy to na prostym przykładzie zadania:
Zadanie 1: Czy do funkcji wyrażonej wzorem y = 3x + 1 należy punkt P(2 ; 7) ?
Autor pyta nas się czy do funkcji należy podany punkt. PAMIĘTAJ! To pytanie mogłoby brzmieć także: Czy punkt znajduje się na funkcji / czy funkcja przecina ten punkt et cetera. Stawiamy zatem tezę:
Tak, punkt należy do funkcji. Zakładamy więc, że spełnia on podane równanie. Pamiętaj, na chwilę obecną tylko to zakładamy, bo czy mamy rację to dopiero się okaże :)
Skoro wyszliśmy z takiego założenia, że punkt do niej należy to znaczy, że współrzędne punktu możemy śmiało podstawić pod wzór naszej funkcji i dokonać obliczeń:
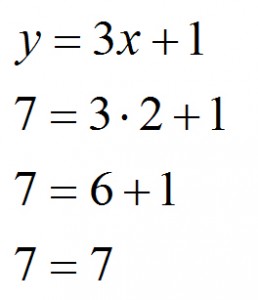
W wyniku końcowym otrzymujemy 7=7 a więc prawdę. Reasumując, można to przetłumaczyć w następujący sposób:
- czy punkt należy do funkcji? (pytanie z treści zadania) - PRAWDA (odpowiedź z naszych obliczeń)
Proste? Proste! Rozwiążmy kolejny przykład:
Zadanie 2:
Czy funkcja określona wzorem y = x – 10 przechodzi przez punkt A o współrzędnych -2 ; 2? Znów podobny przykład jak wyżej. Tak więc stawiamy tezę, że tak i podstawiamy:
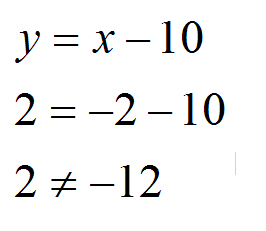
Pytanie: Czy funkcja przechodzi przez punkt?
Odpowiedź: FAŁSZ. 2 nie równa się -12.
Mamy nadzieję, że wszystko jest jasne do tego miejsca :) Tak więc możemy przejść dalej!
Układy równań
Co się dzieje, kiedy nie mamy podanego wzoru funkcji ale znamy dwa punkty w układzie współrzędnych przez które ta funkcja przechodzi? Pokażemy Wam jak rozwiązywać tego typu zadania wraz z prawidłowym tokiem myślenia na przykładzie poniższego zadania.
Zadanie 3:
Podaj wzór funkcji liniowej przechodzącej przez punkty: A(2 ; 4) oraz B(-3 ; 8).
Pytają nas zatem w zadaniu o wzór funkcji. Nie patrzę więc dalej na treść zadania tylko już tutaj zapisuję co wiem i wyciągam wnioski. Skoro proszą o wzór funkcji to go zapiszmy:
y = ax + b
Możemy coś więcej wyłuskać z pierwszej części zdania? Już raczej nie. Więc czytamy dalej. Widzimy, że podali nam jakieś dwa punkty. Nie wiemy co z nimi zrobić więc teraz zastanawiamy się nad naszym wzorem.
No dobra. Mamy wzór y = ax+b. Poproszono mnie, żebym go podał więc muszę obliczyć DWIE niewiadome „a” oraz „b”. No ale jest problem bo w równaniu są jeszcze dwie niewiadome „x” oraz „y”. I tu pytanie: Jak policzyć równanie z dwiema niewiadomymi? Układ równań! Ale… musielibyśmy mieć dwa komplety danych, bo skoro dwie niewiadome do policzenia to na każde z równań po jednym komplecie danych. Co się okazuje? Podano nam je w treści! Punkt A to jeden komplet a punkt B to drugi komplet. Tak więc zapisujemy układ równań i przechodzimy do obliczeń! :)
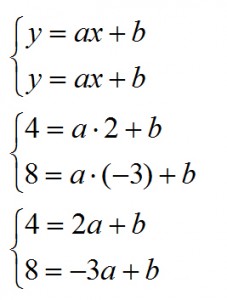
Teraz od jednego równania odejmujemy drugie, żeby pozbyć się niewiadomej „b” czyli wykonujemy następujące operacje:
4 – 8 ; 2a – (-3a) ; b – b
Otrzymujemy:
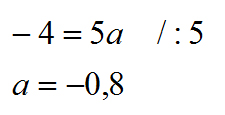
Skoro mamy już policzone „a” to wybieramy sobie DOWOLNE równanie z naszego układu, podstawiamy pod nie nasz współczynnik oraz dowolny punkt A lub B i dokonujemy obliczeń:
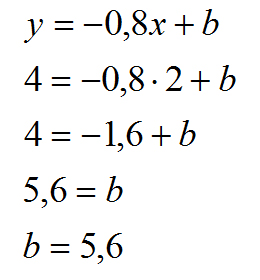
Nasze równanie w wyniku końcowym będzie miało więc postać:
![]()
Możesz we własnym zakresie dokonać sprawdzenia czy punkty faktycznie spełniają podane równanie :) Mamy nadzieję, że układy równań nie będą sprawiały Ci już kłopotów i przekonałeś się, że funkcja liniowa przechodząca przez punkt to temat z którym jesteś sobie w stanie łatwo poradzić. Oczywiście tu zrobiliśmy bardzo proste przykłady, lecz jeśli będziesz stosować podobną zasadę co my tzn. zadawał sobie bardzo proste pytania, zapisywał odpowiedzi na nie w postaci wzorów, dokonywał analizy tego co już masz to uwierz, zrobisz każde zadanie!
To tyle jeśli chodzi o temat Funkcja liniowa przechodząca przez punkt. Zapraszamy do polubienia nas na facebooku i śledzenia kolejnych wpisów!
Poniżej zestaw zadań z zakresu funkcja liniowa przechodząca przez punkt:
POBIERZ ZADANIA - FUNKCJA LINIOWA CZ.5




Komentarze