Funkcja liniowa – część II – przedziały liczbowe

W poprzedniej części przekazaliśmy wam ogólne informacje dotyczące funkcji liniowej. W tej części poruszymy zagadnienie, w którym funkcja liniowa jest ograniczona przedziałem. Zapraszamy do lektury oraz do pobrania naszego zestawu zadań by przećwiczyć nowe umiejętności :)

Czym są przedziały i jak je rozumieć?

Ważne: Przedziały w funkcjach to tak naprawdę ich dziedzina!

Przedziały to „instrukcje warunkowe” - podobnie jak zbiory liczbowe. Przedziały są jednak w stanie dużo dokładniej scharakteryzować liczby, które mają spełniać nasze równanie. Zacznijmy od nawiasów. Stosujemy trzy rodzaje nawiasów do opisania zbioru:

1. klamrowe: { }
2. zamknięte: < > -> w układach współrzędnych oraz osiach liczbowych jako kółko zamalowane
3. okrągłe: ( ) -> w układach współrzędnych oraz osiach liczbowych jako kółko otwarte

Aby lepiej zrozumieć stosowanie powyższych nawiasów będziemy pracować na konkretnym przykładzie funkcji:

y = 6x

1. Powyższa funkcja liniowa przykładowo oblicza nam ile pieniędzy trzeba wypłacić pracownikowi za jego dzień roboczy, gdzie „x” to ilość przepracowanych godzin, a liczba 6 przedstawia jego stawkę godzinową. W wyniku końcowym otrzymujemy obliczoną wartość „y” czyli odpowiedź na pytanie ile w sumie trzeba zapłacić pracownikowi. Przyjmujemy, że pracodawca płaci tylko za pełne godziny pracy i pracownik nie może pracować więcej niż 8 h dziennie. Do opisania więc tej funkcji użyjemy nawiasów { }, które służą aby wymienić konkretne wartości jakie mogą być podstawione pod „x”:{0; 1; 2; 3; 4; 5; 6; 7; 8}Informujemy wtedy kogoś, że jedyne co może wstawić pod „x” to właśnie te liczby czyli, że „x” nie może przyjąć innej wartości niż podane w nawiasach klamrowych.
2. Zmieńmy trochę politykę firmy. Szef okazał się miłosierny i płaci nam za każdą minutę pracy. Nasz przedział może być więc teraz opisany w inny sposób:<0 ; 8>Informujemy wtedy, że za „x” możemy wstawić dowolne wartości zawierające się między 0 a 8 włącznie z 0 oraz 8 tzn. pracownik może danego dnia przepracować 0 godzin lub 1,5 h lub 8 h. W tym wypadku użyjemy właśnie nawiasów zamkniętych.
3. Zmodyfikujmy delikatnie założenia. Pracownik nie może przyjść do pracy na 0 godzin bo to oznacza, że nie ma go wtedy w pracy więc po co w ogóle liczyć jego wynagrodzenie? Reszta pozostaje bez zmian więc przedział będzie opisany tak: (0 ; 8>Oznacza to, że za „x” nie możemy wstawić 0 ale 0,1 już tak i za ten czas pracy będzie należało się wynagrodzenie.

Reasumując więc na czym polega różnica w nawiasach ( ) a < >.

Zapis, który prezentuję poniżej przedstawia dokładnie dwa te same przedziały: < 0 ; 4,(9) > jest dokładnie tym samym przedziałem co < 0 ; 5 )

Spójrzmy na drugą pozycję w nawiasach. 4,(9) to liczba nieskończona gdzie po przecinku w nieskończoność powiela się liczba 9. Liczba ta jest prawie liczbą 5 a dokładniej mówiąc występuje ona bardzo blisko liczby 5 (bliżej już się nie da :)). Prościej w zapisie jest więc zastosować zapis „5)”, który mówi nam, że przedział kończy się PRAWIE na liczbie 5 jednak ostatnią liczbą nie jest 5. Jaka to więc liczba? Ano właśnie 4,(9). Oby dwa te zapisy są zatem prawdziwe, jednak bardziej poprawnym jest zapis krótszy. Tyczy się to całej matematyki. Jeśli coś można zapisać w prostszej postaci to właśnie ona jest bardziej poprawną formą zapisu.

Funkcja liniowa ograniczona przedziałem

Funkcje liniowe poruszane we wcześniejszym wpisie na blogu (część 1) były funkcjami nieskończonymi. Nie posiadały czegoś takiego jak wartość (czyli y) minimalna czy maksymalna. W przypadku funkcji ograniczonych przedziałem dzieje się jednak inaczej. Rozpatrzmy konkretny przykład funkcji:

y = 2x + 4 dziedzina: (-1 ; 1> Narysujmy sobie na początek całą funkcję poprzez obliczenie miejsca zerowego oraz skorzystanie z parametru „b” i połączmy te dwa punkty linią ciągłą (dokładny opis jak to zrobić w poprzedniej części). Po dokonaniu obliczeń uzyskujemy: Mz: -2 Oy: 4 W kolejnym etapie wykreślamy dwie pionowe linie (proste) określające nasz przedział tzn. przez x = -1 oraz x = 1. Twój wykres powinien wyglądać tak:

[caption id="attachment_160" align="aligncenter" width="300"]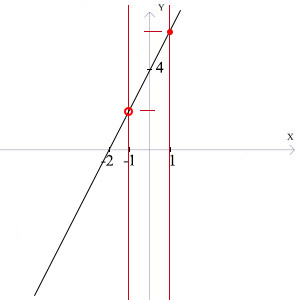 Funkcja liniowa rosnąca w przedziale -1 do 1[/caption]

Ponieważ dziedzina dokładnie określa nam, która część funkcji nas interesuje (gdzie istnieje ona tak naprawdę) reszty w ogóle nie bierzemy pod uwagę. Czyli mimo iż obliczyliśmy miejsce zerowe (tylko na potrzebę zrobienia wykresu) podana funkcja w tej postaci miejsca zerowego nie posiada! Istnieje ona tylko między dwiema czerwonymi prostymi. Można więc odczytać z wykresu, że funkcja ma niby swój „początek” i swój koniec. Początku dokładnie nie jesteśmy w stanie podać bo przy x = -1 funkcja jeszcze nie istnieje (mówi nam o tym dziedzina a na rysunku kółko otwarte). Pisaliśmy o tym przed chwilą. W tym przypadku więc miejscem rozpoczynającym tą funkcję będzie liczba:

-1,00000…….001.

Nie wiemy jaka dokładnie to liczba, prawda? W takim przypadku nie jesteśmy w stanie podać też wartości minimalnej tej funkcji. Jeśli chodzi o koniec funkcji to już sprawa prosta. Ponieważ znamy DOKŁADNIE jaki argument (x) kończy przedział, więc wiemy, że jest to liczba 1 (kółko zamalowane na rysunku). Taka funkcja posiada więc swoją wartość maksymalną.

Jak obliczać wartość minimalną i maksymalną?

Obliczymy to na podstawie powyższego układu współrzędnych. W poprzedniej lekcji pisaliśmy, że każdy punkt składa się z dwóch współrzędnych (x oraz y). Ponieważ znamy wzór funkcji możemy obliczyć jej dokładną wartość w punkcie gdzie x wynosi 1. Podstawiamy więc do wzoru i wykonujemy obliczenia dla x = 1:

y = 2x + 4

y = 2 * 1 + 4

y = 2 + 4

y = 6

Obliczyliśmy dzięki temu wartość maksymalną tej funkcji, która wynosi 6. Zajmijmy się teraz wartością minimalną. Oczywiście jak napisaliśmy wcześniej nie istnieje taka wartość bo nie jesteśmy dokładnie podać jaka to liczba. Możemy jednak powiedzieć PRAWIE jaka to liczba :) Jeśli pod równanie podstawimy za x liczbę -1 będziemy w stanie stwierdzić, że funkcja PRAWIE osiąga tą wartość. Tak więc dokonujemy następujących obliczeń:

y = 2x + 4

y = 2 * (-1) + 4

y = -2 + 4

y = 2

Wiemy więc, że wartość minimalna naszej funkcji to PRAWIE liczba 2. PRAWIE, czyli funkcja nie osiąga tej wartości ale jest bardzo blisko niej np.:

2,0000000….000000001

Funkcja liniowa i jej zbiór wartości

Obliczenia, których dokonaliśmy powyżej posłużą nam do podania odpowiedzi na pytanie, które pada bardzo często: Jaki zbiór wartości posiada dana funkcja liniowa?

Przy funkcjach liniowych nieograniczonych przedziałem zbiór wartości jest zbiorem nieskończonym bo nie występuje wartość minimalna ani maksymalna. W przypadku naszej konkretnej funkcji jest inaczej. Obliczyliśmy, że wartość minimalna to prawie 2 a maksymalna wynosi 6. Posłużymy się więc do opisania tej sytuacji stosując odpowiednie nawiasy:

Zbiór Wartości: (2 ; 6>

Mamy nadzieję, że materiał przekazany w dzisiejszej lekcji pomógł Ci zrozumieć czym są przedziały liczbowe i jak maja się one do funkcji liniowych :)

Zapraszamy do kolejnych lekcji a po skończonym cyklu z funkcji liniowej udostępnimy materiał wideo w którym będziemy rozwiązywać zadania na różnym poziomie trudności.

Zestaw zadań do dzisiejszej lekcji:

POBIERZ ZADANIA