Funkcja liniowa prostopadła oraz funkcja liniowa równoległa nie jednemu z was spędza pewnie sen z powiek. Pokażemy wam, że zupełnie niepotrzebnie a rozwiązywanie takich zadań to żaden problem! :) Tak więc zapraszamy do zapoznania się z artykułem!
Współczynnik kierunkowy prostej
Czym jest współczynnik kierunkowy i o co w nim chodzi? Jak napisaliśmy w poprzednich lekcjach występuje on we wzorze funkcji liniowej w postaci:
y = ax + b
Zapamiętaj, że aby była mowa o współczynniku kierunkowym równanie musi być właśnie w tej postaci! Wiele osób popełnia błąd i dla przykładu kiedy widzi wzór 2y = 4x + 8 to przyjmuje, że współczynnik kierunkowy „a” jest równy 4. NIE JEST TO PRAWDA! Równanie trzeba pierw podzielić obustronnie przez 2 aby po lewej stronie pozostał sam 1 y! Mamy więc wtedy równanie w postaci: y = 2x + 4 gdzie współczynnik wynosi tak naprawdę 2. To samo ma się kiedy widzimy równanie ogólne prostej tzn.:
Ax + By + C = 0
Duża litera „A” nie jest współczynnikiem kierunkowym. Zobaczmy przykład:
4x – 2y + 8 = 0
Najpierw przekształcamy równanie tak aby po lewej stronie zostały same „y” więc przerzucamy elementy stronami do postaci:
-2y = -4x – 8
Dzielimy obustronnie każdy element przez „-2” żeby pozbyć się wszystkiego co stoi przy naszym „y”:
-2y = -4x – 8 /: (-2)
y = 2x + 4
Widać, że współczynnik kierunkowy wynosi więc 2 a nie 4.
Ok. Wiemy już więc co to jest współczynnik kierunkowy i jak go poprawnie odczytywać. Dowiedzmy się więc gdzie go wykorzystywać!
Funkcja liniowa prostopadła
W większości zadań proszą nas aby policzyć funkcję liniową, która jest prostopadła do jakiejś funkcji. Ogólnie warto abyś zapamiętał wzór:
a1 * a2 = -1
No dobrze, ale o co w nim chodzi? Jest to wzór, który wykorzystuje dwa współczynniki kierunkowe z dwóch różnych funkcji. Jeśli znamy którykolwiek z tych współczynników, jesteśmy w stanie policzyć drugi! W praktyce prawie zawsze właśnie od tego powinieneś zacząć wykonywać tego typu zadania.
Dokonujemy więc przekształceń aby wykorzystać wzór do obliczenia współczynnika kierunkowe drugiej funkcji:
a1 * a2 = -1 /: a1
a2 = -1 / a1
Czyli aby obliczyć współczynnik kierunkowy funkcji prostopadłej do naszej funkcji należy po prostu liczbę -1 podzielić przez współczynnik kierunkowy naszej wiadomej funkcji. Drugi sposób, którego można użyć to zastosować dwa proste tricki :) Jeśli wiesz co to liczba odwrotna i liczba przeciwna nie powinieneś mieć kłopotu!
Aby policzyć współczynnik kierunkowy nowej funkcji wystarczy, że na naszym wiadomym współczynniku wykonamy dwa wspomniane wcześniej tricki jednocześnie tzn. zrobimy odwrotność liczby i wstawimy przeciwny znak np. jeśli współczynnik kierunkowy będzie wynosić np. 1/2 to nowy współczynnik będzie jego odwrotnością ( liczbą 2) z przeciwnym znakiem (czyli „-‘’) bo wcześniej był dodatni. Otrzymujemy więc nowy współczynnik o wartości równej: -2 :)
Wychodzi dokładnie to samo co wzorem jednak pamiętaj! Proste sztuczki nie zwalniają Cię z obowiązku znajomości wzorów. Wzory są bardzo ważne i mimo, że są w tablicach matematycznych trzeba je znać, żeby zauważać pewne rzeczy w zadaniach. W końcu na maturze dają wzory, można mieć kalkulatory a mimo to nie zdaje co roku około 25% uczniów.
No dobrze, wiemy już jak liczyć współczynnik kierunkowy nowej funkcji więc zróbmy sobie przykładowe zadanie (wzór funkcji z poprzedniej lekcji):
Zadanie 1:
Podaj wzór funkcji prostopadłej do funkcji o wzorze y = 2x + 4.
[caption id="attachment_215" align="aligncenter" width="300"]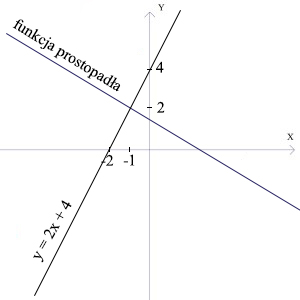
funkcja liniowa prostopadła[/caption]
Ok zaczynamy więc liczyć. Skoro proszą nas o podanie wzoru funkcji liniowej podajmy go już na samym początku!
y = ax + b
Tak właśnie o to chodzi! Po to są wzory aby właśnie od nich wychodzić :) Bardzo naciągana teoria ale można by to uznać za odpowiedź, ponieważ wzór ogólny tyczy się KAŻDEJ funkcji liniowej więc jest to też wzór funkcji o którą pytają no ale wiadomo... dostaniemy zero punktów więc nie robimy sobie żartów z egzaminatora i liczymy dalej ;)
Znając współczynnik kierunkowy pierwszej funkcji za pomocą metody opisanej wcześniej obliczamy nowy współczynnik kierunkowy:
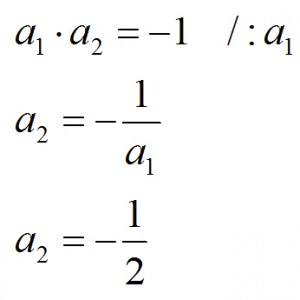
Podstawiamy więc do wzoru (i pamiętaj, że jeśli coś już policzysz podstaw pod wzór a dopiero później zastanawiaj się co dalej z zadaniem):
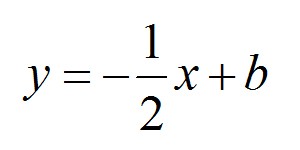
No właśnie. Co z wyrazem wolnym „b” ? Nie możemy go sobie wyczarować znikąd od tak… Analizujemy więc co mamy zapisane w równaniu. Przedstawimy wam nasz sposób rozwiązywania zadań:
Nasz tok myślenia:
„ Ok. Mam równanie z trzema niewiadomymi „x”, „y” oraz „b”. Jak się rozwiązuje równania z taką ilością niewiadomych? Układy równań! No dobra ale musiałbym mieć aż 3 równania skoro mam 3 niewiadome. A tych danych nie mam w zadaniu… Lipa… Ok jedyna opcja jest taka, że skoro muszę obliczyć wyraz wolny b to muszę znać więc jakiś x i jakiś y ale………… „
No właśnie. Musimy znać jakiś „x” oraz „y” żeby móc policzyć „b”. Faktycznie nie zostało nam to dane w treści zadania. Aby był podany „x” oraz „y” w treści musi być podana jeszcze jedna informacja. Musimy wiedzieć, przez jaki punkt w układzie ma przechodzić nasza nowa funkcja liniowa. Dodajmy sobie taką oto treść:
… funkcja liniowa przechodzi przez punkt P ( -1 ; 2 ).
Skoro znamy już naszego „x” oraz „y” to wracamy do obliczeń i najzwyczajniej w świecie podstawiamy :)
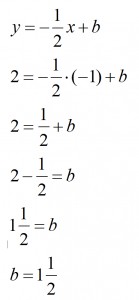
Dzięki temu doszliśmy do końca zadania. Podstawiamy do wzoru naszej nowy funkcji aby w odpowiedzi końcowej otrzymać:
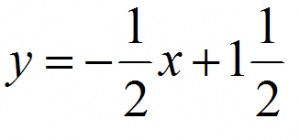
Funkcja liniowa równoległa
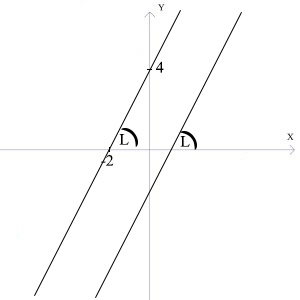
Sprawa z funkcją liniową równoległą jest bardzo podobna do tej z prostopadłą. Skoro jedna funkcja ma być równoległa do drugiej oznacza to, że muszę być one narysowane dokładnie w tym samym kierunku (tzn. być równoległe). I tutaj na logikę: skoro funkcja pierwsza jest równoległa do funkcji drugiej a za kierunek w którym ta funkcja idzie odpowiada nam współczynnik kierunkowy „a” i obie funkcje mają dokładnie TEN SAM kierunek to jaki może być wniosek?
Funkcje równoległe mają zawsze taki sam współczynnik kierunkowy!
Bierze to się stąd, że współczynnik kierunkowy charakteryzuje nam kąt nachylenia funkcji do osi „x”. W funkcjach równoległych kąt ten jest dokładnie taki sam, więc i współczynnik „a” jest taki sam:
Wzór jest prosty i prezentuje się tak:
a1 = a2
Podobnie jak w przypadku funkcji prostopadłej w pierwszej kolejności obliczamy nowy współczynnik kierunkowy a następnie całą resztę.
Zadanie 2:
Podaj wzór funkcji równoległej do funkcji o wzorze y = 2x + 4 i przechodzącej przez punkt P ( 4 ; 1 ).
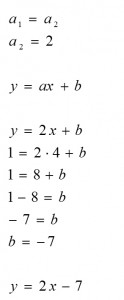
Mamy nadzieję, że od dziś bez problemu będziesz rozwiązywać zadania z funkcjami prostopadłymi i równoległymi.
Poniżej link do zadań abyś przećwiczył dzisiejszy materiał a my zapraszamy do kolejnych lekcji!
Komentarze