Funkcja liniowa z parametrem m - jak ją rozwiązywać? Jeśli to pytanie chodzi Ci po głowie i masz braki w tym temacie lub po prostu chcesz utrwalić zdobytą wiedzę to zapraszamy do zapoznania się z naszym artykułem :)!
Teoria, teoria i jeszcze raz teoria!
Funkcja liniowa z parametrem m to nie czarna magia. Jak w każdym dziale matematyki tak i tutaj, aby poprawnie rozwiązywać zadania trzeba mieć wiedzę teoretyczną i umiejętnie się do niej odwołać. Aby szybko i poprawnie rozwiązywać zadania zajrzyj najpierw do wcześniejszych lekcji jeśli jeszcze ich nie opanowałeś. Naprawdę musisz zrozumieć, że jest to szalenie istotne i że teoria idzie z praktyką w parze :)
Funkcja liniowa z parametrem m
Poniżej przedstawimy kilka przykładowych zadań z tej materii wraz z ich rozwiązaniem oraz tokiem myślenia, którym powinieneś się kierować podczas rozwiązywania zadań!
Zadanie 1.
Dla jakiego parametru „m” podana funkcja jest funkcją rosnącą: y = (m-8)x – 5
Zostawmy na boku funkcję, która została nam podana. Istotniejsze od niej jest „wyłuskanie” z treści o co dokładnie chodzi autorowi:
„… funkcja jest funkcją rosnącą … ‘’
Tutaj musimy w pierwszej kolejności skupić swoją uwagę i odwołać się do wiedzy, którą posiadamy ZAPOMINAJĄC o funkcji podanej w zadaniu. Kiedy funkcja jest rosnąca? Ano wtedy kiedy jej współczynnik jest większy od 0! Jeśli chodzi o matematykę będę powtarzał wam to zawsze :) Zawsze zaczynaj zadania od wzorów! Tak więc to co udało nam się ustalić po prostu zapisujemy:
a > 0
Dobrze, ale co dalej? Wzór który zapisaliśmy tyczy się każdej funkcji liniowej, więc jest on także prawdziwy dla funkcji podanej w naszym zadaniu! Gdzie jest nasz współczynnik kierunkowy „a”?
Przypomnijmy sobie wzór:
y = ax + b
Aha. Współczynnik „a” jest połączony znakiem mnożenia z niewiadomą „x”. Wnioskuję więc, że skoro tak jest to w naszym konkretnym przypadku skoro „x” jest połączony mnożeniem z całym nawiasem, zatem:
a = m – 8
Podstawiamy więc pod naszą nierówność, którą ułożyliśmy:
a > 0
m-8 > 0
a następnie rozwiązujemy:
m > 8
Odpowiedzią na nasze zadanie jest, że aby funkcja była rosnąca (czyli, żeby jej współczynnik kierunkowy był dodatni) za niewiadomą „m” należy wstawić dowolną liczbę większą od 8. Prawda, że nie jest ciężkie? Spróbujmy rozwiązać inne zadanie.
Zadanie 2.
Dla jakiego parametru „m” podana funkcja liniowa nie posiada miejsc zerowych?
![]()
Podobnie jak w poprzednim zadaniu. Zapominamy o podanej funkcji i odwołujemy się do teorii. Kiedy funkcja nie posiada miejsc zerowych? Wtedy, kiedy nie przecina osi X więc musi być funkcją stałą. Kiedy funkcja liniowa jest stała? Wtedy kiedy jej współczynnik kierunkowy jest równy 0!
Tak więc skoro mamy słowny opis naszego równania to korzystamy ze wzoru i obliczamy podstawiając dane z naszej funkcji:
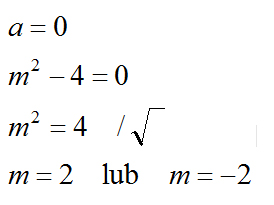
Pamiętaj, że przy operacji kiedy obydwie strony równania pierwiastkujemy a z lewej strony nasza niewiadoma jest podniesiona do potęgi PARZYSTEJ to ZAWSZE muszą wyjść nam dwa rozwiązania!
Spróbujmy zadanie innego typu, nie mieszając już współczynnika kierunkowego :)
Zadanie 3
Dla jakiego parametru „m” podana funkcja liniowa jest większa od 0 w przedziale (-5 ; +oo) ?
y = 2x + m
Mimo, że dla wielu osób zadanie to może sprawić kłopot pamiętajmy, żeby myśleć logicznie nad zadaniem, analizować je krok po kroku i odwoływać się do teorii! To naprawdę proste! :)
Żeby lepiej zrozumieć treść i dane jakie autor nam przekazał sporządźmy sobie rysunek pomocniczy. Wiemy, że współczynnik kierunkowy jest dodatni a zatem funkcja rośnie. Znamy też miejsce zerowe tej funkcji: -5. Ano właśnie. Skąd je znamy? Z przedziału, który został nam podany w treści zadania. Jeśli funkcja liniowa jest rosnąca i autor powiedział nam, że jest ona większa od zera (tzn. że część tej funkcji znajduje się powyżej osi X od miejsca -5) wiemy więc, że miejscem zerowym jest właśnie ta liczba. Sporządźmy rysunek (pamiętaj, rysunek nie musi być dokładny, ma spełniać tylko obrazowo dane które znasz aby pomóc zrozumieć istotę zadania):
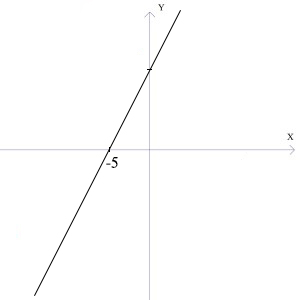
Rysunek, który sporządziliśmy już dokładnie spełnia założenia zadania. Jednak nadal nie wiemy jakie ma być nasze „m”. Zastanówmy się więc czym jest dodatkowy punkt, który nam powstał (mowa tu o punkcie przecięcia z osią Y). Jest to punkt, który we wzorze oznaczony jest jako „b”. Wiemy więc, że nasze „m” tak naprawdę to jest wyraz wolny „b”. Analizujemy więc nasz rysunek pod tym kątem. Jakie musi być „b”, żeby funkcja była cały czas rosnąca? Bo warunek jakim jest przedział od -5 do +00 jest spełniony cały czas. Sprawa rozchodzi się teraz właśnie o wyraz wolny. Odpowiedź jest prosta! Współczynnik „b” musi być dodatni! Gdyby wynosił 0 to podana funkcja była by funkcją stałą pokrywającą się z osią X. Wyklucza taką sytuację równanie, gdzie współczynnik kierunkowy jest większy od 0 więc funkcja MUSI być rosnąca. Podobnie ma się sprawa z ujemną częścią osi Y. Nasze „b” nie może być ujemne bo funkcja byłaby wtedy malejąca. Wniosek?
b > 0
więc:
m także musi być od niego większe.
Rozwiązaniem jest więc zbiór liczb całkowitych dodatnich!
Mamy nadzieję, że dzięki powyższej lekcji jeszcze lepiej zrozumiałeś materiał z zakresu funkcja liniowa z parametrem m.
Poniżej do pobrania zbiór zadań abyś mógł przećwiczyć samemu zadania przedstawione w dzisiejszej lekcji!






Komentarze