Funkcje liniowe – część I – Informacje ogólne

Dla niektórych czarna magia. Innym przysparza niemałych trudności. Mawiają, że tylko wybrańcy potrafią rozwiązać każde zadanie :) W kilku kolejnych artykułach postaramy się wytłumaczyć czym są funkcje liniowe, byście nie mieli z nią problemu w przyszłości i byli w stanie rozwiązać każde zadanie w którym występuje. Do każdego artykułu dołączamy zestaw zadań treningowych w formie PDF! Zaczynamy!

Funkcje liniowe - porady ogólne

Pamiętaj, że jeśli jesteś w stanie coś sobie przy rozwiązywaniu jakiegoś zadania narysować to po prostu to zrób. Rozwiązując zadania z funkcji (i nie tylko) nie skupiaj się na tym co masz osiągnąć w wyniku końcowym. Skup się na tym co zostało Ci podane przez autora i poprawnie to zinterpretuj! Jeśli będziesz sporządzać rysunki pomocnicze będziesz w stanie przy wielu zadaniach „wpaść” na rozwiązanie właśnie dzięki rysunkowi :) Na początku zapamiętajmy, że Y to wartość a X to argument.

Czym są funkcje liniowe?

Zapomnij o definicji książkowej! Ważne, żebyś zrozumiał funkcję liniową a nie wykuł regułkę. Nie tędy droga. Funkcja jest najzwyklejszym równaniem, które posiada lewą i prawą stronę oraz występują w niej dwie niewiadome: X oraz Y. Znając jedną z tych dwóch niewiadomych jesteśmy w stanie policzyć ile musi wynosić w takim razie druga aby równanie było prawdziwe. Przyjrzyjmy się takiemu oto przykładowi:

y + x = 10

Załóżmy, że X to cena talerza a Y to cena filiżanki. Ponieważ nie znamy, żadnej z niewiadomych to wariantów cenowych dających w wyniku końcowym kwotę 10 zł jest nieskończenie wiele. Z tego właśnie względu funkcja liniowa nie ma właśnie początku ani końca. Wymyślając jeden parametr uda nam się ZAWSZE dobrać taki drugi aby wynik końcowy się zgadzał.

Jeśli powiem Ci, że talerz kosztuje 6 zł to ile będzie kosztowała filiżanka? 4 zł! Prawda, że proste? Właśnie to jest główne zastosowanie funkcji. Znając jeden parametr obliczamy ile musi wynosić ten drugi.

Funkcja jest jednak specyficznym równaniem. Doprowadzając powyższą funkcję do postaci w której Y jest po lewej stronie otrzymujemy:

Y = 10 – x (przestawmy X przed 10)

Y = -x +10

Otrzymujemy równanie funkcji liniowej.

Funkcje liniowe - wzór ogólny

Wzór ogólny takiej funkcji ma postać:

Y = ax + b

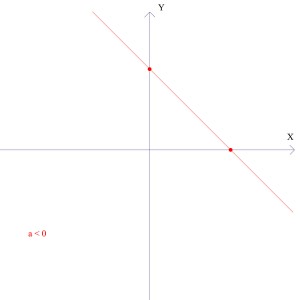
a – tzw. współczynnik kierunkowy, określa czy funkcja rośnie czy maleje. Jeśli „a” jest dodatnie to funkcja rośnie, jeśli „a” jest ujemne to funkcja maleje, natomiast kiedy „a” jest równe 0 (w takim przypadku w równaniu nie występuje niewiadoma X ponieważ ax wynosi wtedy 0 * x co daje 0) funkcja jest stała. Patrz rysunki poniżej:

b – tzw. wyraz wolny. Warto zapamiętać, że wyraz wolny funkcji to ZAWSZE jej miejsce przecięcia z osią Y!

funkcja malejąca np.: y = -2x + 3

funkcja stała np.: y = 6

funkcja rosnąca np.: y = 3x + 4

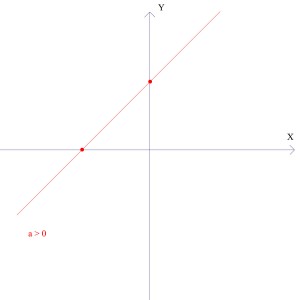
Zauważ, że na każdym z rysunków zaznaczyłem dwa punkty. Proszę by weszło to Ci w nawyk. Wszystko co się przecina, ma jakieś punkty wspólne jest istotne praktycznie we wszystkich zadaniach i warto sobie zadać pytanie co to jest za punkt!

Miejsce zerowe funkcji

Punkty oznaczone na osi X to tak zwane miejsce zerowe tej funkcji. Ponieważ każdy punkt składa się z dwóch współrzędnych X oraz Y to ułatwia nam sprawę, gdyż w takim razie każdy punkt na osi X ma Y = 0 dlatego, że cała oś X przechodzi przez oś Y właśnie w tym miejscu. Taki punkt po podstawieniu do naszego równania powinien nam je wyzerować! Na przykład jeśli funkcja:

Y = 3x + 3 ma miejsce zerowe równe -1 to po podstawieniu tej liczby pod X powinniśmy otrzymać 0.

Sprawdźmy:

Y = 3 * (-1) + 3

Y = -3 + 3

Y = 0

Ok. Wiemy jak sprawdzić czy dana liczba jest miejscem zerowym funkcji ale jak je policzyć jeśli go nie znamy? Są dwa sposoby:

Sposób 1:

W miejsce Y wstaw zero, ponieważ jak stwierdziliśmy wcześniej każdy punkt na osi X posiada Y równe 0 na przykład:

Y = 5x – 10

0 = 5x – 10

10 = 5x /:5

2 = x

Miejsce zerowe powyższej funkcji wynosi 2.

Sposób 2:

Istnieje wzór na miejsce zerowe funkcji liniowej:

Miejsce zerowe = -b : a

zatem:

Mz = -b : a

Mz = -(-10) : 5

Mz = 10 : 5

Mz = 2

Warto byś znał obydwie metody. Pamiętaj, że wzory i metody to Twoje narzędzia pracy z zadaniami. Im więcej ich znasz tym prościej rozwiążesz dane zadanie. Mechanik ponoć młotkiem i śrubokrętem da radę naprawić większość rzeczy ale więcej narzędzi sprawi, że jego praca będzie wydajniejsza, prawda :) ?

Czy punkt należy do funkcji liniowej?

Czy punkt leży na wykresie funkcji, czy punkt należy do funkcji, czy funkcja przechodzi przez punkt….. wszystkie te pytania oznaczają dokładnie to samo. Jeśli dowolny punkt składa się z dwóch współrzędnych X oraz Y to jeśli należy do równania funkcji tzn. że możemy te dane podstawić pod równanie. Nawet jeśli nie należy też możemy to zrobić :) Po prostu zakładamy, że należy a w wyniku końcowym otrzymamy prawdę np.: 3=3 lub fałsz 2 = 8

Przykład:

Czy punkt o współrzędnych (-2 ; 2) należy do wykresu funkcji y = 2x + 1 ?

Sprawdzenie:

2 = 2 * (-2) + 1

2 = -4 + 1

2 = -3

Wniosek:

Ponieważ wyszła nieprawda tzn. że podany punkt nie należy do tej funkcji! Zadaliśmy sobie pytanie i podstawiliśmy dane a na końcu otrzymaliśmy odpowiedź FAŁSZ.

Rysowanie wykresu

Żeby narysować linię prostą potrzebujemy znać przynajmniej dwa jej punkty. Nie ma sensu liczyć ich na „oślep” skoro zostały podane nam już powyżej :) Tak naprawdę, żeby szybko narysować funkcję wystarczy skorzystać tylko ze znajomości współczynnika „b” i nanieść go na oś Y a za pomocą wzoru obliczyć miejsce zerowe. Voilà! Mamy dwa punkty, które łączymy linią prostą. Dla sprawdzenia upewnij się, że funkcja spełnia warunek dla swojego współczynnika kierunkowego i jeśli np. jest on ujemny czy na pewno wyszła Ci funkcja malejąca :)

Jak widzicie funkcje liniowe nie są takie straszne :) Na koniec zapraszamy do pobrania naszego PDF, znajdującego się poniżej i przećwiczenia dzisiejszego materiału.