Dziś omówimy liczby rzeczywiste, naturalne, całkowite, wymierne i niewymierne. Dużo osób pomija zupełnie ten dział, nie przykładając do niego należytej uwagi. Co jednak jeśli z pozoru błahe zadanie będzie posiadało warunek, że odpowiedzi muszą zawierać się w konkretnym zbiorze liczbowym? No właśnie, stracimy punkty na sprawdzianie lub egzaminie a przecież nie o to chodzi :) Poniżej przedstawię Ci jak ZROZUMIEĆ (a nie wykuć) czym są zbiory i o co w nich chodzi.
Liczby rzeczywiste
Zbiór oznaczany literą: R
Z czym kojarzy się słówko „rzeczywiste”? Z rzeczywistością. A co w niej występuje? WSZYSTKO! To dokładnie przedstawia ten zbiór. Jest to zbiór, który zawiera wszystkie liczby jakie tylko istnieją w rzeczywistości. Mówiąc bardziej fachowo zbiór ten zawiera w sobie wszystkie pozostałe zbiory. Poniżej kilka przykładów liczb rzeczywistych:
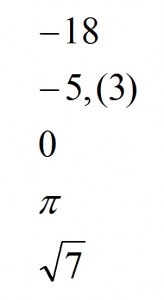
Liczby naturalne
Zbiór oznaczany literą: N
Zapamiętaj, że liczby naturalne to takie, jakie występują w naturze (myślę tu o wszystkim co nie zostało wytworzone przez człowieka). Widziałeś kiedyś, żeby wyrosło pół drzewa? Ok, pewnie pomyślisz, że ścięte też się liczą, jednak mówimy tylko o tym co jest NATURALNE, a ściąć drzewo coś musiało. Wniosek?
W liczbach naturalnych nie może być ściętego drzewa czyli ułamka np.: 1/2 lub 1/3 bo naturalnie taka sytuacja nie może mieć miejsca! Tym bardziej do tego zbioru nie zaliczają się pierwiastki czy liczby stałe np. liczba π (PI).
Może się zdarzyć, że czegoś niema więc 0 jest jak najbardziej naturalne. Tak więc doszliśmy do tego, że liczby naturalne to liczby: 0 , 1 , 2 , 3 ... 90... itd. Tak, zero jest liczbą naturalną.
Warto też dodać, że czasem na potrzeby zadania interesuje nas zbiór liczb naturalnych ale z wyłączeniem liczby zero. Zapisuje się go wówczas w następujący sposób: N+ co oznacza, że interesują nas liczby naturalne dodatnie a zero nie jest liczbą dodatnią.
Liczby całkowite
Zbiór oznaczany literą: C
Jak nazwa wskazuje, są to liczby całe, którym nic nie brakuje wiec nie są ułamkami. Mówiąc wprost jest to identyczny zbiór co zbiór liczb naturalnych jednak zawiera także liczby przeciwne (czyli ujemne) do nich o czym musisz pamiętać! Np. -4 ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; 4...itd.
Liczby wymierne i niewymierne
Liczby wymierne: W
Liczby niewymierne: NW
Liczby wymierne z kolei to takie liczby, które można w pewien sposób „odmierzyć”. Do tego celu służą właśnie ułamki, które pokazują tę miarę np.:
1/2 - czytamy jako: 1 do 2
Często widziałeś pewnie w przepisach kucharskich zapis "1/2", co należy rozumieć właśnie jako zapis miary np.: jedna szklanka mąki na dwie szklanki wody.
Przykładem liczby wymiernej może być również skala na mapie (tak, skala na mapie to także ułamek!). Spójrzmy:
Przykładową skalę 1 : 3000 - czytamy jako "1 do 3000".
Liczbami wymiernymi są więc wszystkie liczby, które można zapisać za pomocą ułamka zwykłego. Są to więc wszystkie ułamki, liczby całkowite a także ułamki dziesiętne o rozwinięciu dziesiętnym okresowym.
Sprawdźmy: 1,(3) można zapisać jako ułamek zwykły w postaci: 1 oraz 1/3. Tak samo jest z wszystkimi innymi ułamkami okresowymi.
Do liczb niewymiernych natomiast zaliczamy wszystkie pozostałe liczby (czyli liczby które nie są liczbami wymiernymi) - na przykład pierwiastki:
![]()
których nie można zapisać w postaci liczby całkowitej a także liczba π (PI).
Do czego służą zbiory liczbowe?
Jak już wspomniano na początku, w zadaniach matematycznych często spotyka się dodatkowe warunki. Można by to nazwać swoistą dodatkową instrukcją, która może przybrać następującą postać:
![]()
Taki zapis oznacza, że: x należy do zbioru liczb naturalnych.
To tak jakbyś koledze powiedział:
- Ej słuchaj! Za swoją niewiadomą „x” wstaw sobie co tylko chcesz, tylko pamiętaj, że musi to być liczba NATURALNA.
W praktyce oznacza to, że wszystkie wyniki jakie nam wyjdą w tym zadaniu jako x, MUSZĄ być liczbą naturalną, gdyż w przeciwnym wypadku wynik będzie traktowany jako nieprawda i nie zostanie zaliczony jako prawidłowa odpowiedź.
I to już koniec tematu Liczby rzeczywiste, naturalne, całkowite, wymierne i niewymierne. Zapraszamy do czytania kolejnych wpisów!






Komentarze